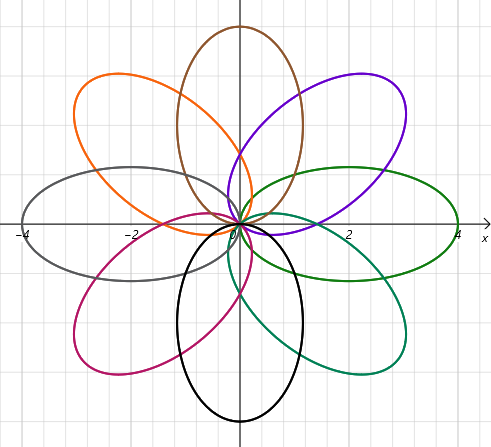
معادلات مورد نیاز
$$\pm{{\sqrt{4-(x-2)^2 \over 3}}}$$
$$2 \pm \sqrt{-3x^2+4}$$
$$\pm{{\sqrt{4-(x+2)^2 \over 3}}}$$
$$-2 \pm \sqrt{-3x^2+4}$$
𝑥^2−𝑥𝑦+𝑦^2−√2 𝑥−√2 𝑦=0
$${{x+\sqrt{2}}\pm \sqrt{-3x^2+6x\sqrt{2}+2}} \over2$$
𝑥^2+𝑥𝑦+𝑦^2+√2 𝑥−√2 𝑦=0
$${-{x-\sqrt{2}}\pm \sqrt{-3x^2+6x\sqrt{2}+2}} \over2$$
𝑥^2−𝑥𝑦+𝑦^2+√2 𝑥+√2 𝑦=0
$${{-x+\sqrt{2}}\pm \sqrt{-3x^2-6x\sqrt{2}+2}} \over2$$
𝑥^2+𝑥𝑦+𝑦^2−√2 𝑥+√2 𝑦=0
$${{x-\sqrt{2}}\pm \sqrt{-3x^2-6x\sqrt{2}+2}} \over2$$
در GeoGebra ببینید (TeX)
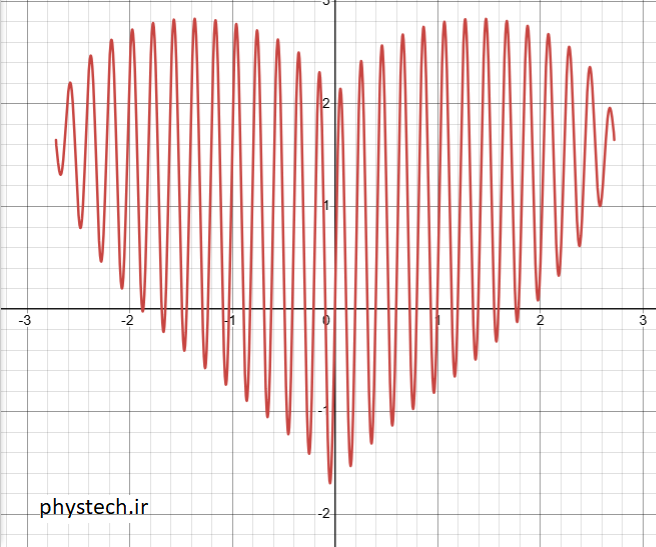
$$sin(\pi ^3x) {\sqrt{e^2-x^2\over 2} }+\sqrt{|x|}$$
- ۰ نظر
- ۳۰ بهمن ۰۳ ، ۱۴:۵۳